Description of processes in the Phyto-DSS
Plant transpiration is the cornerstone of phytomanagement and therefore forms the foundation of the Phyto-DSS. The Phyto-DSS uses potential evapotranspiration (ETo) that is calculated from solar radiation, temperature, relative humidity and wind-speed using the FAO Penman-Monteith equation (Allen et al., 1998). When there is no water stress, crop evapotranspiration (ETc) is the product of ETo and a crop factor (Kc). Kc is dependent on the species and its stage of development. At canopy closure, the maximum Kc values (Kcmax) for most species is between 0.8 and 1.2, with pasture having a Kcmax of 1.0 (Allen et al., 1998). The Phyto-DSS calculates Kc as a fraction of Kcmax depending on the biomass of the crop as a fraction of the biomass at canopy closure, i.e. maximum interception of sunlight. In deciduous trees, Kc is also dependent on the developmental stage of the leaves.
The Phyto-DSS calculates water availability in the substrate from the substrate’s water retention properties. Water extractable at -1 bar (or a nominated soil-water content) or greater, is considered readily available for plant-uptake. Transpiration reduces progressively as the substrate dries out and the extractable water availability falls from -1 bar to -15 bars (or nominated soil-water contents). Water that is extractable at <-15 bars is considered unavailable for plant-uptake. The Phyto-DSS calculates plant-water uptake by dividing the substrate into 1 cm slices, each having a specific root density, water retention curve, and water content. The Phyto-DSS assumes that water uptake activity is greater in substrate layers that have more readily available water. In times of mild drought where the substrate surface is dry, deeper roots become preferentially more active.
The movement of water and solutes in the substrate is calculated using a tipping-bucket approach similar to that described in Hutson and Wagenet (1993). In this method, the substrate is divided into slices, with each slice having specific water retention properties, water content, solute content and a partition coefficient for the solute in the substrate – substrate solution equilibrium. Rainfall or irrigation that infiltrates the soil, increases the water content of successive soil layers to <0.1 bar, then the ‘excess’ substrate solution migrates to the next layer down (Fig. 1). For any substrate, a percentage of the substrate solution will migrate down macropores of 2 or more soils ‘slices’ in length.
Component accumulation as a function of transpiration and soluble component
Soil solution is drawn from the root zone through the plants’ roots and stems to the leaves, where it is lost via transpiration. Any component taken up in the soil solution that enters the roots will accumulate in either the roots or the shoots of the plant. High component concentrations in the roots can result from plant water uptake inducing component migration, via mass flow, to the root surface where they are precipitated (Zhao et al., 2000). Not surprisingly, in the above-ground portions, the highest concentrations are often found in the leaves as they are the major water sink. It is well documented that component translocation from the roots to the shoots is driven by plant water uptake (Salt et al., 1995b; Hinchman et al., 1996). The Phyto-DSS considers the amount of component (M) removed by the plant is therefore proportional to the transpiration rate (T) over a given period of time (t).
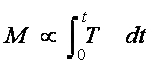 [1]
[1]
Any water that the plant roots take up must first pass though the surrounding soil. During this time, only some fraction of the component present in the bulk soil will be in solution (Echevarria et al., 1998; Gérard et al., 2000). The remainder is likely to be bound to mineral particles and the organic matter in the soil. So bound it is therefore unavailable for uptake. Hence, the total amount of component that accumulates in the plant is proportional, although not directly, to the component concentration that is in the soil solution (Robinson et al., 1997ab; Robinson et al., 1998; Robinson et al., 2000), rather than the total component concentration in the bulk soil. Thus, we consider that M is a function the component concentration in soil solution (C).
![]() [2]
[2]
Root Absorption Factor
The total amount of component that accumulates in the plant does not usually equal the accumulated product of the soil-solution concentration times the volume of water transpired by the plant. For a component to be translocated to the aerial parts of a plant, it has to enter the root, either via the symplastic or apoplastic (Marschner, 1995) pathways where some active or passive filtering may occur.
Here we define the root absorption factor (f) as a dimensionless lumped parameter that represents the root xylem / soil solution component concentration quotient.
 [3]
[3]
where [C]r is the soluble component concentration (mg/L) in the root xylem and [C] is the soluble component concentration (mg/L) in the soil solution.
The parameter f is a simple lumped parameter intended to remove the need to measure the plethora of complex, and often poorly understood, biogeochemical factors that influence the passage of components from the soil into the roots. Rhizobiological activity, root exudates, temperature, moisture, pH and the concentration of competing ions will affect f. The issue is further complicated by the fact that f could change depending on the component concentration in the soil solution. This would be particularly pronounced for essential elements such as iron, copper, zinc and manganese.
Root Absorption Factor and plant responses to heavy metals
Baker (1981) divided plants species into three groups according to their above-ground metal concentrations in relation to the metal concentration in the soil. These three groups are delineated in our model using f. For non-essential elements such as cadmium, nickel and arsenic, plants having a very low f (active exclusion) are termed as being “excluders”. Most plants that occur naturally on metalliferous soils are recognised as being excluders.
Plants that have a relatively constant f over a wide range of metal concentrations in soil solution are known as “indicators”. In this case, the concentration in the plant has a near linear relationship to the metal concentration in soil solution. Plants that do not occur naturally on metalliferous soils usually behave as ‘indicators’ when grown in the presence of the non-essential elements.
The third category of plants are those who tolerate very high concentrations of metal in their aerial parts or have an active uptake mechanism for the non-essential metal (high f). These plants are known as “hyperaccumulators”.
For both excluders and hyperaccumulators, f is constant over just a narrow concentration range. There can be a sudden increase in plant metal concentration at high soil-solution concentrations. At this point, the metal uptake control mechanisms break down, and metal ‘floods’ into the plant in the transpiration stream. The actual phenomenon may be an overload of the regulatory mechanism, or a break down of the plasma membrane at the apoplast/symplast interface. When this phenomenon occurs, the plants show toxicity symptoms and biomass production is reduced.
This change in f over a concentration range can be modelled by adding a decay constant K
 [4]
[4]
where f(C) equals root adsorption factor at soil solution concentration C (mg/L), f1 equals the measured root adsorption factor at concentration C1 (mg/L), and K (0 < K <1) is the decay constant.
Estimating the Root Absorption Factor
The plant specific f can be approximated using the plant’s total water use, above-ground dry biomass, and the component concentration in soil solution. We assume the following relationship holds
 [5]
[5]
f equals the Root Absorption Factor for the component (dimensionless) M equals the component concentration in the above-ground dry biomass (mg/kg), B equals above-ground dry biomass (kg), T equals the total water use (L) and C equals the concentration of component in soil solution (mg/L),
Component uptake from soil
The distribution of components in a contaminated soil is never uniform, and in most agricultural soils the highest concentrations are usually found near the soil surface. Urban and industrial soils are usually more heterogeneous with high component concentrations ‘hot spots’ occurring at depth. For simplicity, our DSS considers the soil to be divided into three zones:
1) a ‘contaminated’ zone where the surface soil has the maximum component concentration
2) an ‘intermediate’ zone where there is a mixing of contaminated and uncontaminated soils.
3) an ‘uncontaminated’ zone where the soil is unaffected by contamination and assumed to have ‘background’ levels for the components.
Phytoextraction induced change in soil component concentration over time
The local concentration of component in soil solution and hence the potential amount of component entering the plant roots, will be depth-dependent. The plant-root density also varies with depth. Most of the plant roots are near the surface and root density decreases with increasing depth. We assume potential component uptake depends on root density.
Plant component-uptake causes a change in soil component concentration (mg/kg) at depth d, and this change is calculated as:
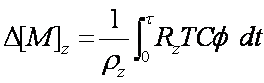 [6]
[6]
where: D[M]z = change in contaminant component concentration (mg/kg) at depth z, rz = bulk density of the soil (g cm-2) at depth z, t = time (days), Rz = root density fraction (root mass at depth z) / (total root mass), T = water use (L/day), C = concentration of component in soil solution (mg/L), f= root absorption factor for the component. The component concentration in soil solution (C) needs to be measured using a consistent physical or chemical techniques such as those described in Ernst (1996). It is imperative that a consistent technique be used, as differing methods will give different values of (C) and therefore f will need to be recalculated [5].
It is clear from the above equation that the phytoextraction process can be enhanced by increasing the concentration of component in the soil solution (C). This may be done by using soil amendments such as chelates.
Alternatively, f or the transpiration rate can be enhanced by selective breeding, or by gene manipulation.
Change in component bioavailability after successive croppings
Over time, as more component is removed from the soil by successive croppings, the soluble component concentration will decrease. In some situations, the change may be approximately linear, however in most cases there could be a logarithmic decay upon successive annual croppings (Robinson et al., 1999).
Return of components to the soil via leaf-fall
If phytoextraction is utilising trees with a cropping rotation of greater than one year, then it can be assumed that the leaves are being recycled back onto the ground and their associated component is being reincorporated into the bulk soil at the surface. The effect of plant biomass re-entering the soil can concentrate even more component in the upper soil profile. The low mobility of heavy-metals in the soil means that as successive generations of leaves are dropped, there can be an accumulation of metals near the surface. This might then be readily removed simply by Surface Scraping. It could, however, also provide a new exposure pathway for the metals (Perronnet et al., 2000).
Limitations of the model
The model [6] is analytically simple, yet has a rationally convenient description of the whole plant-component uptake processes. Environmental conditions that may prohibit plant-growth, such as drought, are not considered. Root absorption factors for component-uptake by a given species could well be different when the plant is grown in different soils. This is because at a single solution concentration, the ease with which a component enters the plant’s symplast will be affected by the cocktail of ions that are present in soil solution, as well as other factors such as soil pH, moisture and temperature.
Upon entering the root, the Phyto-DSS assumes that all the component will be translocated to the above-ground portions of the plant. Analysis of the root material invariably shows that this assumption is not correct due to the presence of the component in the root tissue. Stephan and Scholz (1993) demonstrated that components in the aerial plant parts could be further translocated within in the phloem. Any relocation of components back to the below-ground portions via the phloem will result in an over estimation of the amount of component that is extracted.
The depth-wise distribution of fine roots does not always equate with total root uptake, even for water. Roots tend to be more active when the surrounding soil is moist (Clothier and Green, 1997). The model, for simplicity and utility, considers a uniform moisture distribution in the soil. Given these shortcomings, the model may indicate a slightly shorter time for remediation than actually occurs in the field. Caution must therefore be applied, especially in a commercial sense, to not mislead clients on the necessary time for remediation.
Economic viability: Is phytomanagement the most cost-effective solution?
Phytomanagement must meet two basic criteria. Firstly, it must satisfy environmental legislation. The plants must be able to grow to minimise the risk of contaminant movement offsite from the affected zone. Secondly, phytomanagement will only be used if it is an economically attractive option for the organisation responsible for the land’s remediation or the land’s owner.
To determine the economic viability of phytomanagement it must be compared to the best alternative technology and the economic cost of inaction. Phytomanagement will be implemented only if it is the most financially attractive long-term option.; The Phyto-DSS determines the cost of phytomanagement, V, (US$) by:
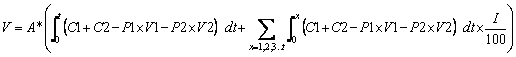 [7]
[7]
where A = total area (ha) C1 = cost of planting (US$ ha-1), C2 = cost of production (US$ / ha), P1 is the production of saleable biomass (t/ha), V1 is the value of the biomass (US$/t), P2 is the production of bio-ore (t/ha) and V2 is the value of the bio-ore (US$/t) and I = interest rate (%).
The Phyto-DSS compares the cost of phytomanagement with the cost of the best alternative technology over the same period. If the alternative technology results in the land being remediated in a shorter period, then the cost of this technology (Va) will be offset by the now-enhanced earnings off the land.
 [8]
[8]
where A = total area (ha), t1 = time needed for conventional technology to remediate land (yr), t2=time taken for phytoextraction to remediate land (yr), C = cost of alternative technology (US$ ha-1), I = interest rate (%) and L = earnings off the land (US$).
The cost of these two technologies must also to be compared with the cost of doing nothing. The cost of inaction is largely due to legislation, however, loss of income off the land, reputation / goodwill, and any future costs will play a role. The value of reputation / goodwill can be difficult to quantify, as it is highly dependent on the stakeholder. Reputation / goodwill may include anything from the political cost of inaction through to loss of earnings due to the refusal of other countries to import produce. Future costs may also be significant if the contaminant is mobile and has the potential to affect groundwater, or other land areas. The cost of inaction (Vi) compared to phytomanagement may be determined by:
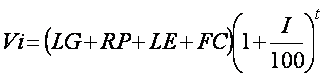 [9]
[9]
where LG = cost of legislation (US$), RP = the cost of loss of reputation/goodwill ($US), LE=loss of earnings off the land (US$ yr-1), FC = future costs (US$), I = interest rate (%) and t=the time simulated for phytomanagement.
References
Allen RG, Pererira LS, Raes D, Smith M 1998 Crop evapotranspiration. Guidelines for computing crop water requirements. FAO irrigation and drainage paper No. 56. FAO, Rome.
Baker AJM 1981 Accumulators and excluders – strategies in the response of plants to heavy metals. Journal of Plant Nutrition 3, 643–654.
Clothier BE and Green SR 1997 Roots: the big movers of water and chemical in soil. Soil Science 162(8), 534–543.
Echevarria G, Morel J L, Fardeau J C and Leclerc-Cessac E 1998 Assessment of phytoavailability of nickel in soils. J. Environmental Quality 27, 1064–1070.
Ernst WHO 1996 Bioavailability of heavy metals and decontamination of soils by plants. Applied; Geochemistry 11, 163–167.
Gérard E, Echevarria G, Sterckeman T and Morel J L 2000 Cadmium availability to three plant species varying in cadmium accumulation pattern. Journal of Environmental Quality 29, 1117–1123.
Hinchman RR, Negri CM and Gatliff EG 1996 Phytoremediation: using green plants to clean up contaminated soil, groundwater and wastewater. Proceedings of the International Topical Meeting on Nuclear and Hazardous Waste Management, Spectrum 96. Seattle WA.
Hutson JL, Wagenet RJ 1993 A pragmatic field-scale approach for modelling pesticides. Journal of Environmental Quality 22, 494-499.
Marschner H 1995 Mineral Nutrition of Higher Plants. Academic Press, London, UK. 65 pp.
Perronnet K, Schwartz C, Gérard E and Morel J L 2000 Availability of cadmium and zinc accumulated in the leaves of Thlaspi caerulescens incorporated into the soil. Plant and Soil 227, 257–263.
Robinson BH, Chiarucci A, Brooks RR, Petit D, Kirkman JH, Gregg PEH and De Dominicis V 1997a The nickel hyperaccumulator plant Alyssum bertolonii as a potential agent for phytoremediation and the phytomining of nickel. Journal of; Geochemical Exploration 59, 75–86.
Robinson BH, Brooks RR, Howes AW, Kirkman JH and Gregg PEH 1997b The potential of the high-biomass nickel hyperaccumulator Berkheya coddii for phytoremediation and phytomining. Journal of Geochemical Exploration 60, 115–126.
Robinson BH, Leblanc M, Petit D, Brooks RR, Kirkman JH and Gregg P E H 1998 The potential of Thlaspi caerulescens for phytoremediation of contaminated soils. Plant and Soil 203,47–56.
Robinson BH, Brooks RR, Gregg PEH and Kirkman JH 1999 The nickel phytoextraction potential of some ultramafic soils as determined by sequential extraction. Geoderma 87, 293–304.
Robinson BH, Mills TM, Petit D, Fung LE, Green SR and Clothier BE 2000 Natural and induced cadmium-accumulation in poplar and willow: Implications for phytoremediation. Plant Soil 227, 301–306.
Salt DE, Prince RC, Pickering IJ, and Raskin I 1995b Mechanisms for cadmium mobility and accumulation in Indian mustard. Plant Physiology 109, 1427-1433.
Zhao FJ, Lombi E, Breedon T, McGrath SP. 2000. Zinc hyperaccumulation and cellular distribution in Arabidopsis halleri. Plant, Cell and Environment 23: 507–514.